Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
Giải:
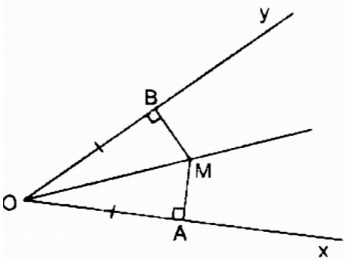
Xét hai tam giác vuông MOA và MOB: \(\widehat {MAO} = \widehat {MBO} = {90^0}\)
OA = OB (gt)
Advertisements (Quảng cáo)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \widehat {AOM} = \widehat {BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat {AOM} = \widehat {BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
