Cho góc vuông xOy, điểm A trên tia Oy. Điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào ?

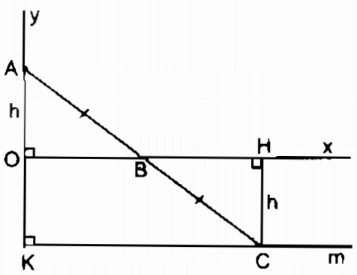
Vì điểm C đối xứng với điểm A qua điểm B ⇒ BA = BC
Kẻ CH ⊥ Ox
Xét hai tam giác vuông AOB và CHB:
\(\widehat {AOB} = \widehat {CHB} = {90^0}\)
Advertisements (Quảng cáo)
BA = BC (chứng minh trên)
\(\widehat {ABO} = \widehat {CBH}\) (đối đỉnh)
Do đó: ∆ AOB = ∆ CHB (cạnh huyền, góc nhọn) ⇒ CH = AO
A, O cố định ⇒ OA không đổi nên CH không đổi.
C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng OA.
Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.
Vậy C chuyển động trên tia Km // Ox, cách Ox một khoảng không đổi bằng OA.
