b. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.. Câu 127 trang 96 Sách bài tập (SBT) Toán 8 tập 1 - Bài 10. Đường thẳng song song với một đường thẳng cho trước
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.
a. So sánh các độ dài AM, DE.
b. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.
Giải:
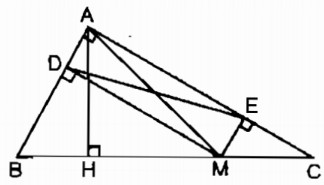
a. Xét tứ giác ADME ta có:
\(\widehat A = {90^0}\) (gt)
MD ⊥ AB (gt)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {MDA} = {90^0}\)
ME ⊥ AC (gt)
\( \Rightarrow \widehat {MEA} = {90^0}\)
Suy ra: Tứ giác ADME là hình chữ nhật (vì có ba góc vuông)
⇒ AM = DE (tính chất hình chữ nhật)
b. Ta có: AH ⊥ BC nên AM ≥ AH. Dấu “=” xảy ra khi M trùng với H.
mà DE = AM (chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC.
