Cho tam giác nhọn ABC có\(\widehat A = {60^0}\), trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a. Chứng minh ∆ BHC = ∆ BMC.
b. Tính \(\widehat {BMC}\)
Giải:
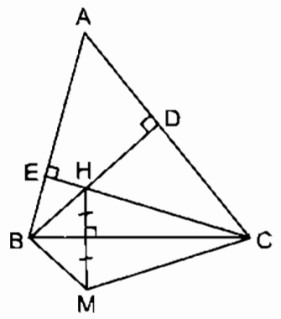
a. Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM ( tính chất đường trung trực)
CH = CM ( tính chất đường trung trực)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)
Advertisements (Quảng cáo)
b. Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E
H là trực tâm của ∆ ABC
⇒ BD ⊥ AC, CE ⊥ AB
Xét tứ giác ADHE ta có:
\(\widehat {DHE} = {360^0} - \left( {\widehat A + \widehat D + \widehat E} \right) \)
\(= {360^0} - \left( {{{60}^0} + {{90}^0} + {{90}^0}} \right) = {120^0}\)
\(\widehat {BHC} = \widehat {DHE}\) (đối đỉnh)
∆ BHC = ∆ BMC (chứng minh trên)
\( \Rightarrow \widehat {BMC} = \widehat {BHC}\)
Suy ra: \(\widehat {BMC} = \widehat {DHE} = {120^0}\)
