Chứng minh rằng AC + CB < AM + MB.. Câu 63 trang 87 Sách bài tập (SBT) Toán 8 tập 1 - Bài 6. Đối xứng trục
Cho hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy (AB không vuông góc với xy). Gọi A’ là điểm đối xứng với A qua xy, C là giao điểm của A’B và xy. Gọi M là điểm bất kì khác C thuộc đường thẳng xy. Chứng minh rằng AC + CB < AM + MB.
Giải:
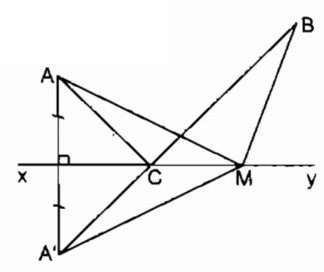
Vì A’ đối xứng với A qua xy
⇒ xy là đường trung trực của AA’
⇒ CA’ = CA (tính chất đường trung trực)
Advertisements (Quảng cáo)
MA = MA’ (tính chất đường trung trực)
AC + CB = A’C + CB = A’B (1)
MA + MB = MA’ + MB (2)
Trong ∆ MA’B ta có:
A’B < A’M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB