Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng:
a. AE song song CF
b. DK \( = {1 \over 2}\)KC
Giải:
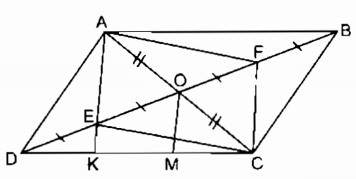
a. Ta có: OB = OD (tính chất hình bình hành)
OE \( = {1 \over 2}\)OD (gt)
OF \( = {1 \over 2}\)OB (gt)
Suy ra: OE = OF
Xét tứ giác AECF, ta có:
OE = OF (chứng minh trên)
OA = OC (vì ABCD là hình bình hành)
Advertisements (Quảng cáo)
Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường ) ⇒ AE // CF
b. Kẻ OM // AK
Trong ∆ CAK ta có:
OA = OC ( chứng minh trên)
OM // AK ( theo cách vẽ)
⇒ CM // MK (tính chất đường trung bình của tam giác) (1)
Trong ∆ DMO ta có:
DE = EO (gt)
EK // OM
⇒ DK // KM (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: DK = KM = MC ⇒ DK \( = {1 \over 2}\)KC
