Cho hình bình hành ABCD có\(\widehat A = \alpha > {90^0}\). Ở phía ngoài hình bình hành, vẽ các tam giác đều ADF, ABE.
a. Tính \(\widehat {EAF}\)
b. Chứng minh rằng tam giác CEF là tam giác đều.
Giải:
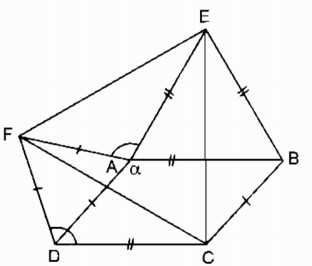
a. Vì \(\eqalign{ & \widehat {BAD} + \widehat {BAE} + \widehat {EAF} + \widehat {FAD} = {360^0} \cr & \Rightarrow \widehat {EAF} = {360^0} - \left( {\widehat {BAD} + \widehat {BAE} + \widehat {FAD}} \right) \cr} \)
mà \(\widehat {BAD} = \alpha \) (gt)
\(\widehat {BAE} = {60^0}\) (∆ BAE đều)
\(\widehat {FAD} = {60^0}\) (∆ FAD đều)
nên \(\widehat {EAF} = {360^0} - \left( {\alpha + {{60}^0} + {{60}^0}} \right) = {240^0} - \alpha \)
b. Ta có: \(\widehat {ADC} + \widehat {BAD} = {180^0}\) (hai góc trong cùng phía bù nhau)
\(\eqalign{ & \Rightarrow \widehat {ADC} = {180^0} - \widehat {BAD} = {180^0} - \alpha \cr & \widehat {CDF} = \widehat {ADC} + \widehat {ADF} = {180^0} - \alpha + {60^0} = {240^0} - \alpha \cr} \)
Suy ra: \(\widehat {CDF} = \widehat {EAF}\)
Advertisements (Quảng cáo)
Xét ∆ AEF và ∆ DCF:
AF = DF (vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
\(\widehat {CDF} = \widehat {EAF}\) (chứng minh trên)
Do đó ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
\(\widehat {ADC} = \widehat {ABC}\) (tính chất hình bình hành)
\(\widehat {CBE} = \widehat {ABC} + {60^0} = \widehat {ADC} + {60^0} = {180^0} - \alpha + {60^0} = {240^0} - \alpha \)
Xét ∆ BCE và ∆ DCF:
BE = CD (vì cùng bằng AB)
\(\widehat {CBE} = \widehat {CDF} = {240^0} - \alpha \)
BC = DF (vì cùng bằng AD)
Do đó: ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra : EF = CF = CE. Vậy ∆ ECF đều.
