Cho tứ giác ABCD. Chứng minh rằng tổng hai góc ngoài tại các đỉnh A và C bằng tổng hai góc trong tạo các đỉnh B và D

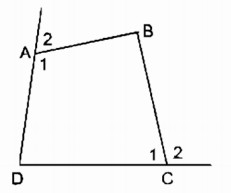
Gọi \(\widehat {{A_1},}\widehat {{C_1}}\) là góc trong của tứ giác tại đỉnh A và C. \({\widehat A_2},{\widehat C_2}\) là góc ngoài tại đỉnh A và C.
Ta có: \({\widehat A_1} + {\widehat A_2} = {180^0}\) (2 góc kề bù)
\(\Rightarrow {\widehat A_2} = {180^0} - {\widehat A_1}\)
\({\widehat C_1} + {\widehat C_2} = {180^0}\) (2 góc kề bù)
Advertisements (Quảng cáo)
\( \Rightarrow {\widehat C_2} = {180^0} - {\widehat C_1}\)
Suy ra:
\(\eqalign{
& {\widehat A_2} + {\widehat C_2} = {180^0} - {\widehat A_1} + {180^0} - {\widehat C_1} \cr
& = {360^0} - \left( {{{\widehat A}_1} + {{\widehat C}_1}} \right) \cr}\) (1)
Trong tứ giác ABCD ta có:
\({\widehat A_1} + \widehat B + {\widehat C_1} + \widehat D = {360^0}\) (tổng các góc của tứ giác)
\(\Rightarrow \widehat B + \widehat D = {360^0} - \left( {{{\widehat A}_1} + {{\widehat C}_1}} \right)\) (2)
Từ (1) và (2) suy ra: \({\widehat A_2} + {\widehat C_2} = \widehat B + \widehat D\)
