Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?. Câu 77 trang 89 Sách bài tập (SBT) Toán 8 tập 1 - Bài 7. Hình bình hành
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Giải:
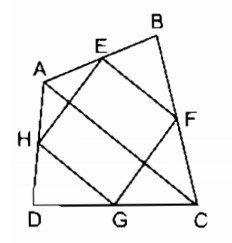
Nối đường chéo AC.
Trong ∆ ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của ∆ ABC
Advertisements (Quảng cáo)
⇒ EF // AC và EF \( = {1 \over 2}\)AC (tính chất đường trung bình tam giác) (1)
Trong ∆ ADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG \( = {1 \over 2}\)AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)