Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.. Câu 9 trang 80 Sách bài tập (SBT) Toán 8 tập 1 - Bài 1. Tứ giác
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.

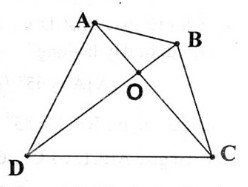
Gọi O là giao điểm của hai đường chéo AC và BD.
Trong ∆OAB, ta có:
OA + OB > AB (bất đẳng thức tam giác) (1)
Advertisements (Quảng cáo)
Trong ∆OCD, ta có:
OC + OD > CD (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2):
OA + OB + OC + OD > AB + CD
⇒ AC + BD > AB + CD
