Hoạt động1
Trong bài toán nêu ở phần mở đầu, hãy viết:
a) Các biểu thức \(A\left( x \right),\,\,B\left( x \right)\) lần lượt biểu thị (theo \(x\)) tổng khối lượng các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải;
b) Hệ thức thể hiện sự bằng nhau của hai biểu thức trên.

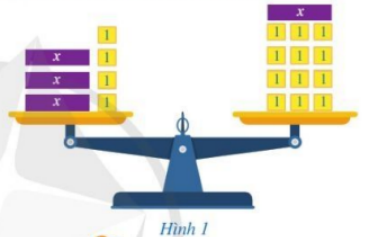
Dựa theo số lượng các hộp màu tím và hộp màu vàng ở hai bên cân để viết biểu thức \(A\left( x \right),\,\,B\left( x \right)\) biểu thị (theo \(x\)) tổng khối lượng ở mỗi đĩa cân.

a)
- Ta thấy ở đĩa cân bên trái có 3 hộp màu tím mỗi hộp có khối lượng \(x\) kg và 4 hộp màu vàng mỗi hộp có khối lượng 1 kg nên biểu thức biểu diễn tổng khối lượng các hộp xếp ở đĩa cân bên trái là:
\(\begin{array}{l}\,\,\,\,\,\,\,A\left( x \right) = 3.x + 4.1\\ \Rightarrow A\left( x \right) = 3x + 4\end{array}\)
Advertisements (Quảng cáo)
- Ta thấy ở đĩa cân bên phải có 1 hộp màu tím mỗi hộp có khối lượng \(x\) kg và 12 hộp màu vàng mỗi hộp có khối lượng 1 kg nên biểu thức biểu diễn tổng khối lượng các hộp xếp ở đĩa cân bên phải là:
\(\begin{array}{l}\,\,\,\,\,\,B\left( x \right) = 1.x + 12.1\\ \Rightarrow B\left( x \right) = x + 12\end{array}\)
b) Biểu thức thể hiện sự bằng nhau của hai biểu thức trên là: \(3x + 4 = x + 12\)
Hoạt động2
Khi \(x = 4\), tính giá trị mỗi vế của phương trình: \(3x + 4 = x + 12\,\,\left( 1 \right)\). So sánh hai giá trị đó.

Thay \(x = 4\) vào từng vế của phương trình rồi tính giá trị mỗi vế.

Thay \(x = 4\) vào vế trái của phương trình ta được: \(3.4 + 4 = 12 + 4 = 16\).
Thay \(x = 4\) vào vế phải của phương trình ta được: \(4 + 12 = 16\).
Ta thấy khi \(x = 4\), hai vế của phương trình có giá trị bằng nhau.
