
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \dfrac{1}{3}BC\)

Áp dụng tính chất trọng tâm G trong tam giác ABC và định lí Thalès vì MG //AB

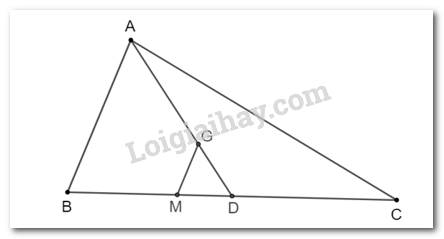
Lấy D là trung điểm của cạnh BC.
Advertisements (Quảng cáo)
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{2}{3}\) hay \(AG = \dfrac{2}{3}A{\rm{D}}\)
Vì MG // AB, theo định lí Thalès, ta suy ra: \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{{BM}}{{B{\rm{D}}}} = \dfrac{2}{3}\)
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên \(\dfrac{{BM}}{{BC}} = \dfrac{{BM}}{{2B{\rm{D}}}} = \dfrac{2}{{2.3}} = \dfrac{1}{3}\)
Do đó \(BM = \dfrac{1}{3}BC\) (đpcm).
