
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.
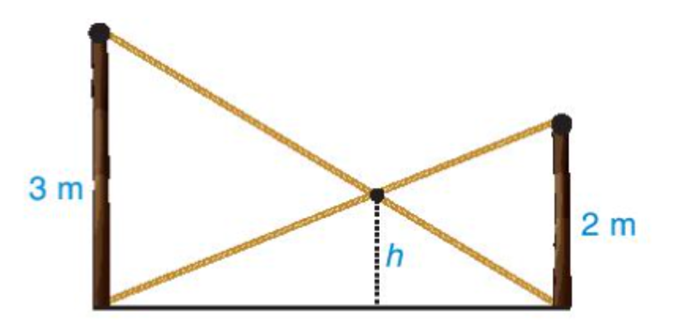

- Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h

Theo đề bài, ta có hình vẽ:
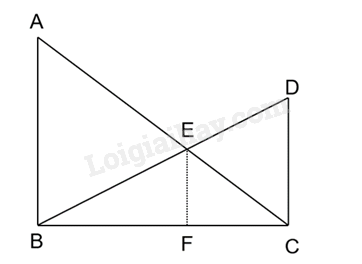
- Có AB // CD
=>\(\widehat {BAC} = \widehat {DCA}\) (2 góc so le trong)
Advertisements (Quảng cáo)
\(\widehat {BDC} = \widehat {AB{\rm{D}}}\)(2 góc so le trong)
- Xét hai tam giác ABE và tam giác CDE, có \(\widehat {BAC} = \widehat {DCA};\widehat {B{\rm{D}}C} = \widehat {AB{\rm{D}}}\)
=> ΔABE ∽ ΔCDE
=>\(\frac{{C{\rm{D}}}}{{AB}} = \frac{{CE}}{{A{\rm{E}}}} = \frac{2}{3}\)
=>\(\frac{{CE}}{{A{\rm{E}}}} = \frac{2}{3}\)=>\(\frac{{CE}}{{CA}} = \frac{2}{5}\)
- Xét hai tam giác CEF và tam giác CAB có EF // AB
=> ΔCEF ∽ ΔCAB (theo định lý)
=>\(\frac{{F{\rm{E}}}}{{AB}} = \frac{{CE}}{{CA}} = \frac{2}{5}\)
=>\(\frac{{F{\rm{E}}}}{{AB}} = \frac{2}{5}\) =>\(\frac{{F{\rm{E}}}}{3} = \frac{2}{5}\)=>\(F{\rm{E}} = 3.\frac{2}{5} = 1,2(m)\)
Vậy độ cao h là 1,2 m
