
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE=4cm, AB=6cm. Chứng minh rằng ΔAEF∽ΔECD và tính tỉ số đồng dạng
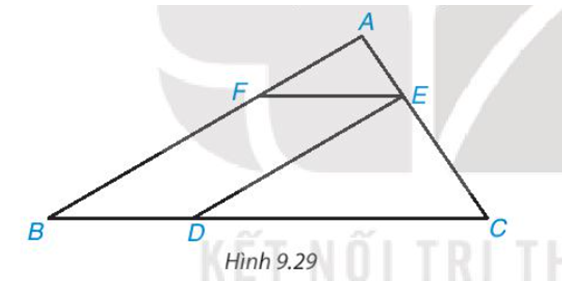

Áp dụng tính chất hai đường thẳng song song => Các cặp góc bằng nhau
=> Hai tam giác đồng dạng, ta có tỉ số đồng dạng

- Có EF // BC =>\(\widehat {{\rm{AEF}}} = \widehat {AC{\rm{D}}}\) (2 góc đồng vị) (1)
- Có EF // BD (vì EF // BC)
Advertisements (Quảng cáo)
DE // FB (vì DE // BC)
=> EFBD là hình bình hành
=>\(\widehat {EFB} = \widehat {E{\rm{D}}B}\)
mà \(\widehat {EFB} + \widehat {{\rm{AFE}}} = {180^o}\)
\(\widehat {E{\rm{D}}B} + \widehat {E{\rm{D}}C} = {180^o}\)
=>\(\widehat {AF{\rm{E}}} = \widehat {E{\rm{D}}C}\) (2)
Từ (1) và (2) => ΔAEF ∽ ΔECD (g.g)
Có \(\frac{{AF}}{{E{\rm{D}}}} = \frac{2}{4} = \frac{1}{2}\)
=> Đồng dạng với tỉ số \(\frac{1}{2}\)
