
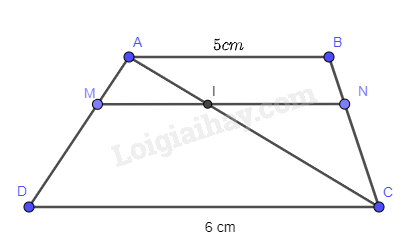
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM=MD, 2BN=NC. Biết AB=5cm,CD=6cm. Hãy tính độ dài đoạn thẳng MN

Gọi I là giao điểm của AC và MN
Sử dụng các tam giác đồng dạng để tính độ dài MI, IN. Từ đó tính độ dài đoạn MN.

Gọi I là giao điểm của AC và MN
Advertisements (Quảng cáo)
Vì 2AM=MD suy ra \(\frac{{AM}}{{M{\rm{D}}}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{A{\rm{D}}}} = \frac{1}{3}\)
Vì 2BN=NC suy ra \(\frac{{BN}}{{NC}} = \frac{1}{2} \Rightarrow \frac{{NC}}{{CB}} = \frac{2}{3}\)
Xét hình thang ABCD có \(\frac{{AM}}{{M{\rm{D}}}} = \frac{{BN}}{{NC}}\) suy ra MN // AB //DC
Xét hai tam giác AMI và ADC có: góc A chung, \(\widehat {AIM} = \widehat {AC{\rm{D}}}\) (do MN// DC)
Suy ra \(\Delta AMI \backsim \Delta A{\rm{D}}C\) suy ra: \(\frac{{AM}}{{{\rm{AD}}}} = \frac{{MI}}{{DC}} = \frac{1}{3} \Rightarrow MI = \frac{1}{3}.DC = \frac{1}{3}.6 = 2(cm)\)
Xét hai tam giác CNI và CBA có góc C chung, \(\widehat {CIN} = \widehat {CAB}\) (do MN // AB)
Suy ra \(\Delta CNI \backsim \Delta CBA\) suy ra: \(\frac{{CN}}{{CB}} = \frac{{NI}}{{BA}} = \frac{2}{3} \Rightarrow NI = \frac{2}{3}.BA = \frac{2}{3}.5 = \frac{{10}}{3}\)(cm)
MN = MI + IN = \(2 + \frac{{10}}{3} = \frac{{16}}{3}(cm)\)
