
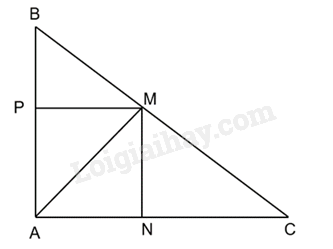
Cho tam giác ABC có AB=6cm, AC=8cm, BC=10cm. Cho điểm M nằm trên cạnh BC sao cho BM=4cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB.
a) Chứng minh ΔBMP ∽ ΔMCN
b) Tính độ dài đoạn thẳng AM

a) Áp dụng trường hợp đồng dạng của hai tam giác vuông.
b) Từ các tỉ số đồng dạng tính ra AP, PM và áp dụng định lí Pythagore để tính AM

a) Ta thấy \(A{B^2} + A{C^2} = B{C^2}\)
=> Tam giác ABC vuông tại A
Có AC ⊥ AB
Advertisements (Quảng cáo)
mà MP ⊥ AB
=> MP // AC
=> \(\widehat {BMP} = \widehat {MCN}\) (2 góc đồng vị)
Xét tam giác vuông BMP (vuông tại P) và tam giác MCN (vuông tại N) có \(\widehat {BMP} = \widehat {MCN}\)
=> ΔBMP ∽ ΔMCN
b) Xét tam giác BMP và tam giác BAC có MP // AC
=> \(\widehat {BMP} = \widehat {BAC}\)
=> \(\frac{4}{{40}} = \frac{{PM}}{8}\)
=> PM=3,2(cm)
=> BP=2,4 (áp dụng định lý Pythagore trong tam giác vuông BMP)
=> AP=3,6 (cm)
=> \(AM = \sqrt {23,2} \)(áp dụng định lý Pythagore trong tam giác vuông AMP)
