
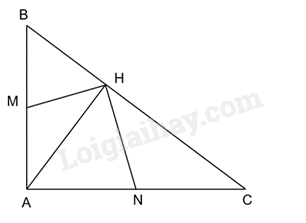
Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM∽ΔHAN

Chứng minh \(\widehat {HAC} = \widehat {ABC} = \widehat {ABH}\) và \(\frac{{HB}}{{HA}} = \frac{{BM}}{{AN}}\) suy ra ΔHBM∽ΔHAN

\(\begin{array}{l}\Delta BAC \backsim \Delta BHA\left( {\widehat A = \widehat H;{{\widehat B}^{}}\ chung} \right)\\ \Rightarrow \frac{{BA}}{{BH}} = \frac{{AC}}{{HA}} \Rightarrow \frac{{HB}}{{HA}} = \frac{{BA}}{{AC}}(1)\end{array}\)
\(\begin{array}{l}\Delta BAC \backsim \Delta AHC\left( {\widehat A = \widehat H,{{\widehat C}^{}}chung} \right)\\ \Rightarrow \widehat {HAC} = \widehat {ABC}(2)\end{array}\)
Advertisements (Quảng cáo)
Vì M là trung điểm của AB nên \(\frac{{BM}}{{BA}} = \frac{1}{2}\)
Vì N là trung điểm của AC nên \(\frac{{AN}}{{AC}} = \frac{1}{2}\)
\( \Rightarrow \frac{{BM}}{{BA}} = \frac{{AN}}{{AC}} \Rightarrow \frac{{BM}}{{AN}} = \frac{{BA}}{{AC}}(3)\)
Từ (1), (3) suy ra: \(\frac{{HB}}{{HA}} = \frac{{BM}}{{AN}}\)
Xét hai tam giác HBM và HAN có:
\(\widehat {HAC} = \widehat {ABC} = \widehat {ABH}\)
\(\frac{{HB}}{{HA}} = \frac{{BM}}{{AN}}\)
\( \Rightarrow \Delta HBM \backsim \Delta HAN\) (c.g.c)
