
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat {ABN} = \widehat {ACM}\)
a) Chứng minh rằng ΔABN ∽ ΔACM
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN=IC.IM

a) Chứng minh: tam giác ABN và tam giác ACM
có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)
=> ΔABN ∽ ΔACM
b) Chứng minh: ΔIBM ∽ ΔICN (g.g) nên suy ra các tỉ số đồng dạng

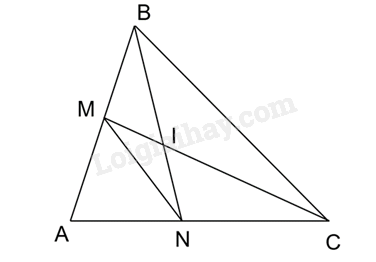
a) Xét tam giác ABN và tam giác ACM
Advertisements (Quảng cáo)
có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)
=> ΔABN ∽ ΔACM
b) Có ΔABN ∽ ΔACM
\(\widehat {ANB} = \widehat {AMC}\)
Có \(\widehat {ANB} + \widehat {CNB} = {180^o}\)
\(\widehat {AMC} + \widehat {BMC} = {180^o}\)
=> \(\widehat {CNB} = \widehat {BMC}\)
Xét tam giác IBM và tam giác ICN
Có \(\widehat {CNB} = \widehat {BMC}\) và \(\widehat {IBM} = \widehat {ICN}\)
=> ΔIBM ∽ ΔICN (g.g)
=> \(\frac{{IB}}{{IC}} = \frac{{IM}}{{IN}}\)
=> IB.IN=IC.IM
