Bài 10. Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai góc vuông với diện tích hình vuông dựng trên cạnh huyền.
Hướng dẫn giải:
Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Advertisements (Quảng cáo)
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4.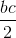 (1)
(1)
SGHIK= (b+c)2 = Sa + 4.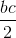 (2)
(2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa
