Bài 4. Cho biết AB\'/AB= AC\'/AC. Bài 4 trang 59 - Sách giáo khoa toán 8 tập 2 - Định lí TaLet trong tam giác
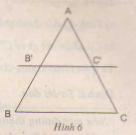
Bài 4. Cho biết \(\frac{AB'}{AB}\) = \(\frac{AC'}{AC}\) (h.6)
Chứng minh rằng:
a) \(\frac{AB'}{B'B}\) = \(\frac{AC}{C'C}\)’
b) \(\frac{BB'}{AB}\) = \(\frac{CC'}{AC}\).
a) Ta có:
Advertisements (Quảng cáo)
\(\frac{AB'}{AB}\) = \(\frac{AC'}{AC}\) => \(\frac{AC}{AC'}\) = \(\frac{AB}{AB'}\)
=> \(\frac{AC}{AC'}\) - 1 = \(\frac{AC-AC'}{AC'}\) = \(\frac{AB-AB'}{AB'}\)
=> \(\frac{CC'}{AC'}\) = \(\frac{B'B}{AB'}\) => \(\frac{AB'}{BB'}\) = \(\frac{AC'}{CC'}\)
b) Vì \(\frac{AB'}{AB}\) = \(\frac{AC'}{AC}\) mà AB’ = AB - B’B, AC’ = AC - C’C.
\(\frac{AB-BB'}{AB}\) = \(\frac{AC -CC'}{AC}\) => 1 - \(\frac{B'B}{AB}\) = 1 - \(\frac{C'B}{AC}\)
=> \(\frac{B'B}{AB}\) = \(\frac{C'B}{AC}\)