Bài 6. Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
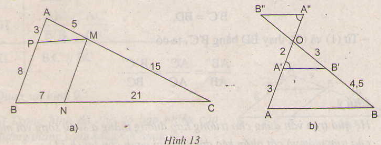

Trên hình 13a ta có:
\(\frac{AP}{PB}\) = \(\frac{3}{8}\); \(\frac{AM}{MC}\)= \(\frac{5}{15}\) = \(\frac{1}{3}\) vì \(\frac{3}{8}\) ≠ \(\frac{1}{3}\) nên \(\frac{AP}{PB}\) ≠ \(\frac{AM}{MC}\) => PM và MC không song song.
Ta có \(\left.\begin{matrix} &\frac{CN}{NB}=\frac{21}{7}=3 \\ & \frac{CM}{MA}=\frac{15}{5}=3 \end{matrix}\right\} => \frac{CM}{MA}=\frac{CN}{NB}\) => MN//AB
Advertisements (Quảng cáo)
Trong hình 13b
Ta có: \(\frac{OA'}{A'A}\) = \(\frac{2}{3}\); \(\frac{OB'}{B'B}\) = \(\frac{3}{4,5}\) = \(\frac{2}{3}\)
=> \(\frac{OA'}{A'A}\) = \(\frac{OB'}{B'B}\) => A’B’ // AB (1)
Mà \(\widehat{B"A"O}\) = \(\widehat{OA'B'}\) lại so le trong
Suy ra A”B” // A’B’ (2)
Từ 1 và 2 suy ra AB // A’B’ // A”B”
