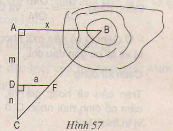
Bài 54. Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách như hình 57. Bài 54 trang 87 - Sách giáo khoa toán 8 tập 2 - Ứng dụng thực tế của tam giác đồng dạng
Bài 54. Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách như hình 57:
AB // DF; AD = m; DC = n; DF = a.
a) Em hãy nói rõ về cách đo như thế nào.
b) Tính độ dài x của khoảng cách AB.

Advertisements (Quảng cáo)
a) Cách đo: Chọn thêm hai điểm C và D sao cho A,D,C thẳng hàng AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thằng hàng và DF ⊥ AC.
b) ∆CDF ∽ ∆CAB (DF // AB)
=> \(\frac{DF}{AB}=\frac{CD}{CA}\) = > AB = \(\frac{DF.CA}{CD}= \frac{a(m+n)}{m}\)
vẫy x= \(\frac{DF.CA}{CD}= \frac{a(m+n)}{m}\)
