Tứ giác ABCD có AB= BC và tia phân giác cưa góc A. Chứng minh rằng ABCD là hình thang.. Bài 9 trang 71 sgk toán 8 tập 1 - Hình thang
9. Tứ giác ABCD có AB= BC và tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.

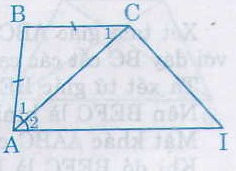
Ta có AB = BC (gt)
Suy ra ∆ABC cân
Advertisements (Quảng cáo)
Nên \(\widehat{A_{1}}=\widehat{C_{1}}\) (1)
Lại có \(\widehat{A_{1}}= \widehat{A_{2}}\) (2) (vì AC là tia phân giác của \(\widehat{A}\))
Từ (1) và (2) suy ra \(\widehat{C_{1}}=\widehat{A_{2}}\)
nên BC // AD (do \(\widehat{C_{1}},\widehat{A_{2}}\) ở vị trí so le trong)
Vậy ABCD là hình thang
