Trả lời câu hỏi Bài 5 trang 73 Toán 8 Tập 2 . Hai tam giác \(ABC\) và \(A’B’C’\) có kích thước như trong hình 32 (có cùng đơn vị đo là xentimet). Bài 5. Trường hợp đồng dạng thứ nhất
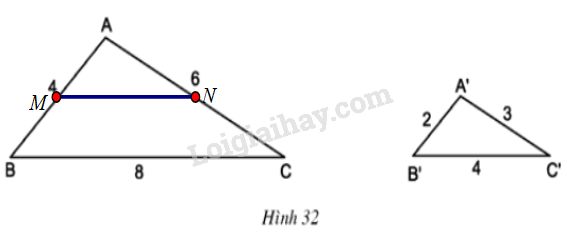
Hai tam giác \(ABC\) và \(A’B’C’\) có kích thước như trong hình 32 (có cùng đơn vị đo là xentimet)
Trên các cạnh \(AB\) và \(AC\) của tam giác \(ABC\) lần lượt lấy hai điểm \(M, N\) sao cho
\(AM = A’B’ = 2cm; AN = A’C’ = 3cm\).
Tính độ dài đoạn thẳng \(MN\).
Có nhận xét gì về mối quan hệ giữa các tam giác \(ABC, AMN, A’B’C’\)?
Áp dụng định lí Ta-lét đảo
Advertisements (Quảng cáo)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{1}{2}\)
\(⇒ MN // BC\) (định lí Ta lét đảo)
\(\eqalign{& \Rightarrow {{AM} \over {AB}} = {{AN} \over {AC}} = {{MN} \over {BC}} = {1 \over 2} \cr & \Rightarrow MN = {1 \over 2}BC = {1 \over 2}.8 = 4 \,cm\cr} \)
Nhận xét:
\(ΔAMN\) đồng dạng \(ΔABC\); \(ΔAMN = ΔA’B’C’\); \(ΔABC\) đồng dạng \(ΔA’B’C’\).