Câu hỏi/bài tập:

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A’M’, B’N’, C’P’ là các đường trung tuyến của tam giác A’B’C’. Biết rằng ΔA’B’C’ ∽ ΔABC
Chứng minh rằng \(\frac{{A}'{M}’}{AM}=\frac{{B}'{N}’}{BN}=\frac{{C}'{P}’}{CP}\).

Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để chứng minh.

Advertisements (Quảng cáo)
Vì ΔA’B’C’ ∽ ΔABC nên: $\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}$ (1), $\widehat{A’B’C’}=\widehat{ABC},\widehat{B’C’A’}=\widehat{BCA},\widehat{C’A’B’}=\widehat{CAB}$ (2).
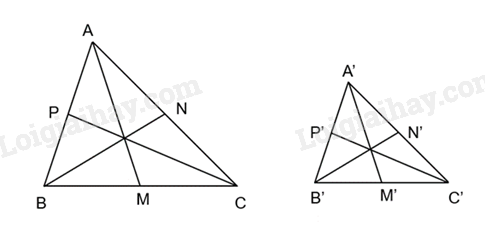
Hai tam giác A’B’M’ và ABM có:
$\frac{B’M’}{BM}=\frac{\frac{B’C’}{2}}{\frac{BC}{2}}=\frac{B’C’}{BC}=\frac{B’A’}{BA}$ (theo (1)),
$\widehat{A’B’M’}=\widehat{A’B’C’}=\widehat{ABC}=\widehat{ABM}$
Suy ra $\Delta A’B’M’\backsim \Delta ABM$(c.g.c). Do đó $\frac{A’M’}{AM}=\frac{A’B’}{AB}$.
Tương tự, \(\Delta B’C’N’\backsim \Delta BCN\) và suy ra $\frac{B’N’}{BN}=\frac{B’C’}{BC},\Delta C’A’P’\backsim \Delta CAP$ và suy ra $\frac{C’P’}{CP}=\frac{A’C’}{AC}$. Từ các đẳng thức trên và (1) ta suy ra $\frac{A’M’}{AM}=\frac{B’N’}{BN}=\frac{C’P’}{CP}$.
