Chứng minh tam giác ABC đồng dạng với tam giác MDC => cặp tỉ lệ cạnh bằng nhau => tính được DC. Trả lời Giải bài 7 trang 98 vở thực hành Toán 8 tập 2 - Bài 36. Các trường hợp đồng dạng của hai tam giác vuông . Cho tam giác ABC vuông tại A có AC = 3cm, BC = 8cm.
Câu hỏi/bài tập:

Cho tam giác ABC vuông tại A có AC = 3cm, BC = 8cm. Đường trung trực của đoạn thẳng BC cắt đường thẳng AC tại một điểm D. Tính độ dài đoạn thẳng CD.

Chứng minh tam giác ABC đồng dạng với tam giác MDC => cặp tỉ lệ cạnh bằng nhau => tính được DC.
Advertisements (Quảng cáo)

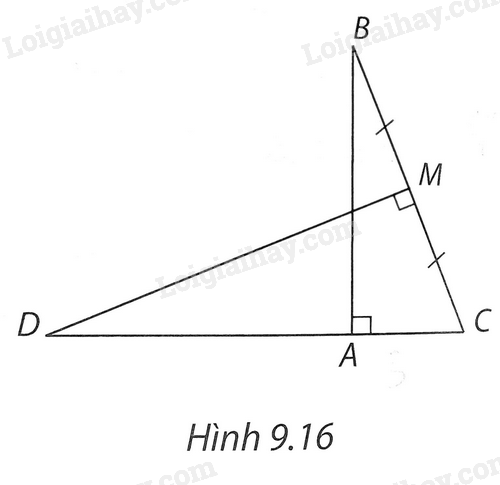
Gọi M là trung điểm của BC. Hai tam giác vuông ABC (vuông tại A) và MDC (vuông tại M) có góc C chung nên $\Delta ABC\backsim \Delta MDC$ (một cặp góc nhọn bằng nhau).
Do đó $\frac{AC}{MC}=\frac{BC}{DC}$, hay $DC=\frac{MC.BC}{AC}=\frac{32}{3}$.
