Câu hỏi/bài tập:

Cho hình vuông ABCD có cạnh bằng 4cm và M, N lần lượt là trung điểm của AB, BC.
Gọi O là giao điểm của CM và DN (H.9.17). Tính độ dài đoạn thẳng OM.
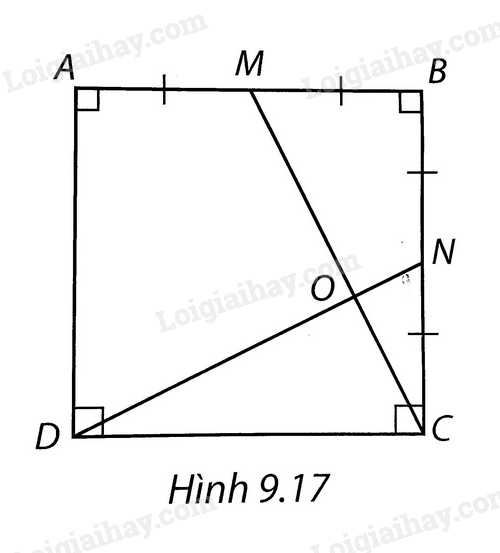

Chứng minh CM $\bot $ DN. Tính diện tích tam giác DMN => OM.

Advertisements (Quảng cáo)
Ta có $\Delta CBM=\Delta DCN$(hai tam giác vuông có hai cặp cạnh tương ứng bằng nhau).
Do đó $\widehat{CNO}+\widehat{NCO}=\widehat{CND}+\widehat{BCM}=\widehat{BMC}+\widehat{BCM}={{90}^{0}}$.
Vì tổng các góc trong tam giác NOC bằng 1800 nên: $\widehat{NOC}={{180}^{0}}-\widehat{CNO}-\widehat{NCO}={{90}^{0}}$.
Suy ra CM vuông góc với DN.
Gọi S là diện tích hình vuông ABCD. Ta có:
${{S}_{\Delta DMN}}=S-{{S}_{\Delta NBM}}-{{S}_{\Delta MAC}}=16-4-2-4=6(c{{m}^{2}})$.
Do vậy OM. DN = $2{{S}_{\Delta DMN}}$. Suy ra $OM=\frac{2{{S}_{\Delta DMN}}}{\sqrt{C{{D}^{2}}+C{{N}^{2}}}}=\frac{12}{\sqrt{16+4}}=\frac{6\sqrt{5}}{5}(cm)$.
