Câu hỏi/bài tập:

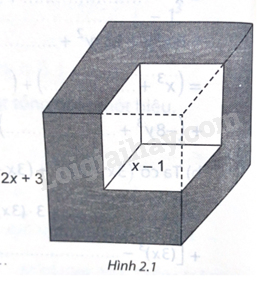
Từ một khối lập phương có độ dài cạnh là \(2x + 3\) (cm), ta cắt bỏ một khối lập phương có độ dài \(x-1\) (cm) (H.2.1). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.

Sử dụng công thức tính thể tích khối lập phương.
Advertisements (Quảng cáo)

Do cạnh của khối lập phương ban đầu là \(2x + 3\) nên thể tích của khối lập phương ban đầu là \({\left( {2x + 3} \right)^3}\).
Thể tích của khối lập phương bị cắt đi là \({\left( {x-1} \right)^3}\).
Thể tích phần còn lại là \({\left( {2x + 1} \right)^3} - {\left( {x - 1} \right)^3}\)
\(\begin{array}{l} = \left[ {{{\left( {2x} \right)}^3} + 3.{{\left( {2x} \right)}^2}.1 + 3.2x{{.1}^2} + {1^3}} \right] - \left( {{x^3} - 3{x^2} + 3x - 1} \right)\\ = 8{x^3} + 12{x^2} + 6x + 1 - {x^3} + 3{x^2} - 3x + 1\\ = \left( {8{x^3} - {x^3}} \right) + \left( {12{x^2} + 3{x^2}} \right) + \left( {6x - 3x} \right) + \left( {1 + 1} \right)\\ = 7{x^3} + 15{x^2} + 3x + 2.\end{array}\)
