Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai. Phân tích, đưa ra lời giải Câu 4 trang 70 - Bài 15. Định lí Thalès trong tam giác - Vở thực hành Toán 8.
Câu hỏi/bài tập:
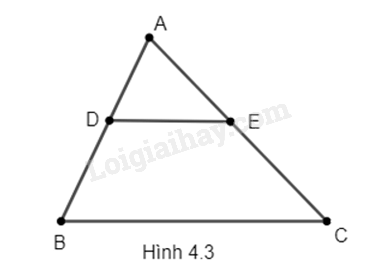
Quan sát Hình 4.3. Biết DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:
A. 20.
B. 56.
C. 45.
D. 50.
Advertisements (Quảng cáo)

Áp dụng định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Áp dụng định lý Thales, ta có: \(\frac{{DB}}{{AB}} = \frac{{CE}}{{AC}}\) Mà AB = AD + DB = 12 + 18 = 30
Khi đó \(\frac{{18}}{{30}} = \frac{{30}}{{AC}} \Rightarrow AC = 30:\frac{{18}}{{30}} = 50.\)
Do đó AC = 50.
=> Chọn đáp án D.
