Câu hỏi/bài tập:

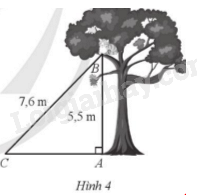
Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cảnh cây với độ cao AB = 5,5 m. Để đưa con mèo xuống, người ta cần phải đặt thang dựa vào cành cây đó. Khoảng cách từ chân thang đến điểm chạm vào cảnh cây là BC = 7,6 m. Góc giữa thang với phương nằm ngang là góc BCA. Tính các tỉ số lượng giác của góc BCA (làm tròn kết quả đến hàng phần trăm).

Bước 1: Áp dụng định lý Pythagore để tính AC.
Bước 2: Dùng các công thức lượng giác để tính các tỉ số lượng giác của góc BCA.

Advertisements (Quảng cáo)
Xét tam giác ABC vuông tại A, ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} \) (Định lý Pythagore)
\(AC = \sqrt {7,{6^2} - 5,{5^2}} = \sqrt {27,51} \left( m \right)\).
\(\sin \widehat {BCA} = \frac{{AB}}{{CB}} = \frac{{5,5}}{{7,6}} = \frac{{55}}{{76}} \approx 0,72\);
\(\cos \widehat {BCA} = \frac{{CA}}{{CB}} = \frac{{\sqrt {27,51} }}{{7,6}} \approx 0,69\);
\(\tan \widehat {BCA} = \frac{{AB}}{{AC}} = \frac{{5,5}}{{\sqrt {27,51} }} \approx 1,05\);
\(\cot \widehat {BCA} = \frac{{AC}}{{AB}} = \frac{{\sqrt {27,51} }}{{5,5}} \approx 0,95\).
