Câu hỏi/bài tập:

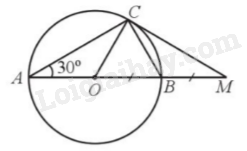
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC, sao cho \(\widehat {CAB} = 30^\circ \). Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh
a) MC là tiếp tuyến của đường tròn (O).
b) \(MC = R\sqrt 3 \).

a) Bước 1: Chứng minh \(CB = OB = BM\).
Bước 2: Dựa vào tính chất: Trong một tam giác, đường trung tuyến ứng với một cạnh và bằng nửa cạnh ấy thì tam giác đó vuông, ta chứng minh được \(CM \bot OC\).
b) Áp dụng tỉ số lượng giác trong tam giác vuông OCM để tính CM.

Advertisements (Quảng cáo)
a) Xét tam giác OAC có \(OA = OC\left( { = R} \right)\) nên tam giác OAC cân tại O, do đó \(\widehat A = \widehat {ACO} = 30^\circ \).
Xét tam giác ABC có \(OA = OB = OC = \frac{{AB}}{2}\left( { = R} \right)\) nên tam giác ABC vuông tại C, nên \(\widehat {ACB} = 90^\circ \).
Ta có \(\widehat {ACO} + \widehat {OCB} = \widehat {ACB} = 90^\circ \), suy ra \(\widehat {OCB} = 90^\circ - \widehat {ACO} = 90^\circ - 30^\circ = 60^\circ \).
Xét tam giác OCB có \(OB = OC\left( { = R} \right)\) và \(\widehat {OCB} = 60^\circ \) nên tam giác OCB đều,
do đó \(OC = OB = CB.\)
Vậy \(OC = OB = CB = BM.\)
Xét tam giác OCM có\(MB = OB = CB = \frac{{OM}}{2}\) nên tam giác OCM vuông tại C,
hay \(CM \bot OC\).
Do đó MC là tiếp tuyến của đường tròn (O).
b) Do tam giác OCM vuông tại C và \(\widehat {COB} = 60^\circ \) nên \(\widehat M = 30^\circ \)
Ta có \(\tan M = \frac{{OC}}{{MC}}\) hay \(MC = \frac{{OC}}{{\tan M}} = \frac{R}{{\tan 30^\circ }} = R\sqrt 3 \).
