Câu hỏi/bài tập:

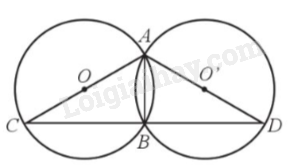
Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). So sánh độ dài dây BC của đường tròn (O) và độ dài dây BD của đường tròn (O’)

Bước 1: Chứng minh \(AC = AD\).
Bước 2: Chứng minh góc ABC và góc ABD vuông.
Bước 3: Chứng minh \(\Delta ABC = \Delta ABD\).

Advertisements (Quảng cáo)
Do 2 đường tròn (O) và (O’) có cùng bán kính R nên 2 đường kính \(AC = AD\).
Góc ABC và góc ABD lần lượt là góc nội tiếp chắn nửa đường tròn tâm O và tâm O’ nên \(\widehat {ABC} = \widehat {ABD} = 90^\circ \).
Xét tam giác ABC và ABD có:
\(\widehat {ABC} = \widehat {ABD}\);
\(AC = AD\);
AB chung
Suy ra \(\Delta ABC = \Delta ABD\) (cạnh huyền – cạnh góc vuông).
Do đó \(CB = DB\).
Vậy độ dài dây BC của đường tròn (O) bằng độ dài dây BD của đường tròn (O’).
