Câu hỏi/bài tập:

Cho đường tròn tâm O đường kính AB và điểm M di chuyển trên đường tròn (M khác A và B). Vẽ đường tròn (M) tiếp xúc với AB tại H. Từ A và B kẻ hai tiếp tuyến AC, BD của đường tròn (M) lần lượt tại C, D.
a) Chứng minh AC + BD không đổi khi M di chuyển trên đường tròn (O).
b) Chứng minh CD là tiếp tuyến của đường tròn (O).

a) Chứng minh \(BD = BH\)và \(CA = AH\), từ đó tính được\(AC + BD\).
b) Bước 1: Chứng minh C, M, D thẳng hàng.
Bước 2: Chứng minh \(\widehat {AMO} = \widehat {MAC}\left( { = \widehat {MAO}} \right)\).
Bước 3: Chỉ ra \(\widehat {AMO} + \widehat {CMA} = \widehat {CMO} = 90^\circ \), từ đó suy ra \(MO \bot CD\).

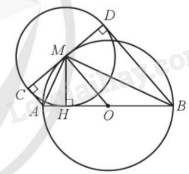
a) Do H là điểm tiếp xúc của (M) và AB nên BH, AH là tiếp tuyến của (M).
Advertisements (Quảng cáo)
Ta có: BD, DH là 2 tiếp tuyến của (M) cắt nhau tại B nên \(BD = BH\).
Ta lại có: AC, HA là 2 tiếp tuyến của (M) cắt nhau tại A nên \(CA = AH\).
Suy ra \(AC + BD = AH + BH = AB\). Mà AB không đổi (là bán kính của (O)) nên AC + BD không đổi.
b) Vì AC, HA là 2 tiếp tuyến của (M) nên \(\widehat {AMC} = \widehat {AMH}\), BD, DH là 2 tiếp tuyến của (M) nên \(\widehat {BMH} = \widehat {DMB}\).
Mà góc AMB là góc nội tiếp chắn nửa đường tròn (O) nên \(\widehat {AMB} = 90^\circ \).
Do đó \(\widehat {AMH} + \widehat {BMH} = \widehat {AMC} + \widehat {DMB} = \widehat {AMB} = 90^\circ \),
suy ra \(\widehat {AMH} + \widehat {BMH} + \widehat {AMC} + \widehat {DMB} = 90^\circ + 90^\circ = 180^\circ \) hay C,M,D thẳng hàng.
Ta có \(\Delta AMO\) cân tại O (do MO, AO là bán kính (O)) nên \(\widehat {AMO} = \widehat {MAO}\).
Mặt khác \(\widehat {MAO} = \widehat {MAC}\) (do AC, AH là tiếp tuyến (M)) nên \(\widehat {AMO} = \widehat {MAO} = \widehat {MAC}\)
mà \(\widehat {MAC} + \widehat {CMA} = 90^\circ \)(\(\Delta CAM\) vuông) nên \(\widehat {AMO} + \widehat {CMA} = \widehat {CMO} = 90^\circ \), suy ra \(MO \bot CM\)
hay \(MO \bot CD\).
Mà OM là bán kính (O), vậy CD là tiếp tuyến của đường tròn (O).
