
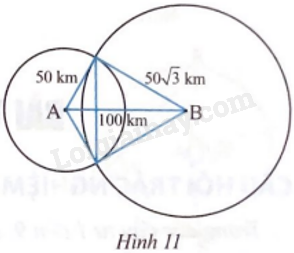
Hai trạm phát sóng A và B đặt cách nhau 100 km. Trạm phát sóng A và trạm phát sóng B có bán kính hoạt động lần lượt là 50 km và \(50\sqrt 3 \) km. Tính diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B. Biết rằng nếu khoảng cách từ thiết bị thu sóng đến trạm phát sóng lớn hơn bán kính hoạt động của trạm phát sóng thì thiết bị không thu được sóng của trạm phát sóng đó.

Dựa vào: Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) được tính bởi công thức: \(S = \pi ({R^2} - {r^2})\).

Gọi C và D là giao điểm của hai đường tròn (A; 50 km) và (B; \(50\sqrt 3 \) km).
Ta thấy AB2 = AC2 + BC2, suy ra tam giác ABC vuông tại C.
Tam giác ABC có sin B =\(\frac{{AC}}{{AB}} = \frac{1}{2}\),
suy ra \(\widehat B = {30^o}\);
Advertisements (Quảng cáo)
suy ra \(\widehat A = {60^o}\),
suy ra \(\widehat {CBD} = {60^o},\) \(\widehat {CAD} = {120^o}\).
Do đó tam giác BCD đều, suy ra CD = \(50\sqrt 3 \) km.
Diện tích hình quạt tròn giới hạn bởi bán kính AC, bán kính AD và cung nhỏ CD của (A; 50 km) là:
\({S_1} = \frac{{\pi {{.50}^2}.120}}{{360}} = \frac{{2500\pi }}{3}(k{m^2})\).
Diện tích hình quạt tròn giới hạn bởi bán kính BD, bán kính BC và cung nhỏ CD của (A; \(50\sqrt 3 \) km) là:
\({S_2} = \frac{{\pi .{{\left( {50\sqrt 3 } \right)}^2}.60}}{{360}} = 1250\pi (k{m^2})\).
Diện tích tứ giác ABCD là:
\({S_{ABCD}} = \frac{1}{2}.AB.CD = \frac{1}{2}.100.50\sqrt 3 = 2500\sqrt 3 (k{m^2})\).
Diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B là:
\({S_1} + {S_2} - {S_{ABCD}} = \frac{{2500\pi }}{3} + 1250\pi - 2500\sqrt 3 \approx 2214,86(k{m^2}).\)
