Câu hỏi/bài tập:

Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết \(AB = 10cm\), \(AC = 7cm\) và \(BC = 6cm\). Tính độ dài của các đoạn thẳng AM, AN, BM và CN.

+ Dựa vào tính chất hai tiếp tuyến cắt nhau ta có \(AM = AN\), \(BM = BE\), \(CE = CN\).
+ \(AM + AN = AB + AC + CE\), từ đó tính được AM, AN.
+ \(BM = AM - AN,CN = AN - CN\).

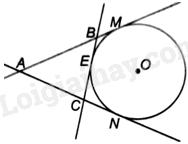
Vì AM và AN là hai tiếp tuyến cắt nhau của (O) nên \(AM = AN\).
Advertisements (Quảng cáo)
Vì BM và BE là hai tiếp tuyến cắt nhau của (O) nên \(BM = BE\).
Vì CE và CN là hai tiếp tuyến cắt nhau của (O) nên \(CE = CN\).
Ta có:
\(AM + AN = AB + BM + AC + CN \)
\(= AB + BE + AC + CE = AB + AC + \left( {BE + CE} \right)\)
\( = AB + AC + BC\)
Suy ra \(2AM = 10 + 7 + 6 = 23\left( {cm} \right)\) nên \(AM = AN = 11,5\left( {cm} \right)\)
\(BM = AM - AB = 11,5 - 10 = 1,5\left( {cm} \right),\)
\(CN = AN - AC = 11,5 - 7 = 4,5\left( {cm} \right)\).
