Câu hỏi/bài tập:

Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB).
a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào?
b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) lần lượt tại C và D. Hãy so sánh các độ dài BC và CD.

a) Chứng minh \(IA = AB - IB\) nên hai đường tròn (I; IB) và (A; AB) tiếp xúc trong.
b) + Chứng minh tam giác ACB vuông tại C, suy ra \(AC \bot CB\).
Advertisements (Quảng cáo)
+ Chứng minh tam giác ABD cân tại A. Do đó, AC là đường cao đồng thời là đường trung tuyến trong tam giác ABD. Do đó, \(BC = CD\).

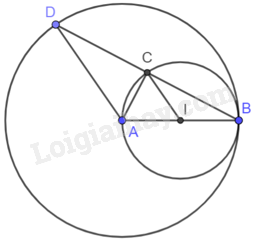
a) Vì I thuộc AB nên \(IA = AB - IB\) nên hai đường tròn (I; IB) và (A; AB) tiếp xúc trong.
b) Tam giác ABC có CI là đường trung tuyến và \(CI = IA = IB = \frac{1}{2}AB\) nên tam giác ACB vuông tại C. Do đó, \(AC \bot CB\).
Vì AB = AD (bằng bán kính của (A; AB)) nên tam giác ABD cân tại A.
Do đó, AC là đường cao đồng thời là đường trung tuyến trong tam giác ABD. Do đó, \(BC = CD\).
