Câu hỏi/bài tập:

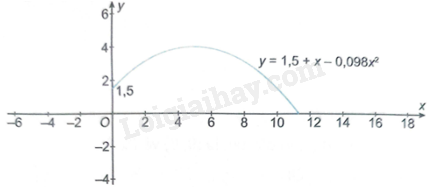
Quỹ đạo chuyển động của một quả bóng được cho bởi công thức \(y = 1,5 + x - 0,098{x^2}\), trong đó y (mét) là độ cao của quả bóng so với mặt đất và x (mét) là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí ném (xem hình bên). Tính khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất.

+ Vật chạm đất khi \(y = 0\), tức là \(1,5 + x - 0,098{x^2} = 0\).
Advertisements (Quảng cáo)
+ Giải phương trình vừa tìm được, lấy giá trị x dương, từ đó rút ra kết luận.

Vật chạm đất khi \(y = 0\), tức là \(1,5 + x - 0,098{x^2} = 0\)
Vì \(\Delta = {1^2} - 4.1,5.\left( { - 0,098} \right) = 1,588 > 0\). Vì \(x > 0\) nên \(x = \frac{{ - 1 - \sqrt {1,588} }}{{2.\left( { - 0,098} \right)}} \approx 11,53\).
Vậy khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí bóng chạm đất là khoảng 11,53m.
