Câu 1.1 trang 100 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho hình bs.4. Biết \(\overparen{DOA}\)= 1200, OA vuông góc với OC, OB vuông góc với OD.
a) Đọc tên các gốc ở tâm có số đo nhỏ hơn 1800.
b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 1800).
d) So sánh hai cung nhỏ AB và BC.
Giải
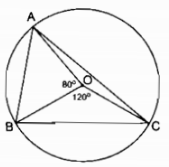
a) Các góc ở tâm có số đo nhỏ hơn 1800 là:
\(\widehat {AOB},\widehat {AOC},\widehat {AOD},\widehat {BOC},\widehat {BOD},\widehat {COD}\)
b) \(OA \bot OC \Rightarrow \widehat {AOC} = {90^0}\)
\(OB \bot OD \Rightarrow \widehat {BOD} = {90^0}\)
\(\widehat {AOB} + \widehat {BOD} = \widehat {AOD}\)
\( \Rightarrow \widehat {AOB} = \widehat {AOD} - \widehat {BOD} = {120^0} - {90^0} = {30^0}\)
\(\widehat {AOC} + \widehat {COD} = \widehat {AOD}\)
\( \Rightarrow \widehat {COD} = \widehat {AOD} - \widehat {AOC} = {120^0} - {90^0} = {30^0}\)
\(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\)
\( \Rightarrow \widehat {BOC} = \widehat {AOC} - \widehat {AOB} = {90^0} - {30^0} = {60^0}\)
c) Các cung có số đo bằng nhau nhỏ hơn 1800 là:
\(\overparen{AB}\) = \(\overparen{CD}\); \(\overparen{AC}\) = \(\overparen{BD}\)
d) sđ \(\overparen{AB}\)=\( = \widehat {AOB} = {30^0}\)
sđ \(\overparen{BC}\)\( = \widehat {BOC} = {60^0}\)
Suy ra: sđ \(\overparen{BC}\) gấp đôi sđ \(\overparen{AB}\)
Câu 1.2 trang 100 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ \(\overparen{BC}\) = sđ \(\overparen{BA}\) ; sđ \(\overparen{BD}\) = \({1 \over 2}\) sđ \(\overparen{BA}\); sđ \(\overparen{BE}\) = \({2 \over 3}\) sđ \(\overparen{BA}\).
a) Đọc tên các góc ở tâm có số đo không lớn hơn 1800.
b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 1800).
d) So sánh hai cung nhỏ AE và BC.
Giải
a) Các góc ở tâm có số đo không quá 1800 là:
Advertisements (Quảng cáo)
\(\widehat {AOB},\widehat {AOC},\widehat {AOD},\widehat {AOE},\widehat {BOC},\widehat {BOD},\)
\(\widehat {BOE},\widehat {COD},\widehat {COE},\widehat {DOE}\)
b) \(\widehat {AOB} = {180^0}\)
sđ \(\overparen{AB}\) = 1800
Ta có: sđ \(\overparen{BC}\) = \( = {1 \over 6}\) sđ \(\overparen{AB}\)
= \({1 \over 6}{.180^0}\) = 300
\( \Rightarrow \widehat {BOC} = \) sđ \(\overparen{BC}\) = 300
Ta có: sđ \(\overparen{BD}\) \( = {1 \over 2}\)sđ \(\overparen{AB}\)
= \({1 \over 2}{.180^0} = {90^0}\)
\( \Rightarrow \widehat {BOD} = \)sđ \(\overparen{BD}\) = \({90^0}\)
Ta có: sđ \(\overparen{BE}\) \( = {2 \over 3}\) sđ \(\overparen{BA}\)
\( = {2 \over 3}{.180^0} = {120^0}\)
\( \Rightarrow \widehat {BOE} = \) sđ \(\overparen{BE}\) = 1200
\(\widehat {BOC} + \widehat {COE} = \widehat {BOE}\)
\( \Rightarrow \widehat {COE} = \widehat {BOE} - \widehat {BOC}\)
\( = {120^0} - {30^0} = {90^0}\)
\(\widehat {AOE} + \widehat {BOE} = \widehat {AOB}\)
\( \Rightarrow \widehat {AOE} = \widehat {AOB} - \widehat {BOE}\)
\( = {180^0} - {120^0} = {60^0}\)
\(\widehat {AOD} = \widehat {BOD} = {1 \over 2}\widehat {AOB} = {90^0}\)
\(\widehat {BOC} + \widehat {COD} = \widehat {BOD}\)
\( \Rightarrow \widehat {COD} = \widehat {BOD} - \widehat {BOC}\)
= \({90^0} - {30^0} = {60^0}\)
\(\widehat {COD} + \widehat {DOE} = \widehat {COE}\)
\( \Rightarrow \widehat {DOE} = \widehat {COE} - \widehat {COD}\)
\( = {90^0} - {60^0} = {30^0}\)
c) Các cung có số đo nhỏ hơn 1800 bằng nhau.
\(\overparen{BC}\)= \(\overparen{DE}\); \(\overparen{AE}\) = \(\overparen{CD}\); \(\overparen{AD}\) = \(\overparen{BD}\).
\(\overparen{AC}\) = \(\overparen{BE}\); \(\overparen{AD}\) = \(\overparen{CE}\); \(\overparen{CE}\) = \(\overparen{BD}\).
d) sđ \(\overparen{AE}\) \( = \widehat {AOE} = {60^0}\)
sđ \(\overparen{BC}\)\( = \widehat {BOC} = {30^0}\)
Ta có số đo của cung \(\overparen{AE}\) gấp đôi số đo của cung \(\overparen{BC}\).
