Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.

Kẻ \(OK \bot CD \Rightarrow CK = DK = {1 \over 2}CD\)
Kẻ \(OH \bot AB \Rightarrow AH = BH = {1 \over 2}AB\)
Vì AB // CD nên H, O, K thẳng hàng.
Áp dụng định lí Pi-ta-go vào tam giác vuông OBH, ta có:
\(O{B^2} = B{H^2} + O{H^2}\)
Suy ra: \(O{H^2} = O{B^2} - B{H^2} = {25^2} - {20^2} = 225\)
OH = 15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ODK, ta có:
Advertisements (Quảng cáo)
\(O{D^2} = D{K^2} + O{D^2}\)
Suy ra: \(O{K^2} = O{D^2} - D{K^2} = {25^2} - {24^2} = 49\)
OK = 7 (cm)
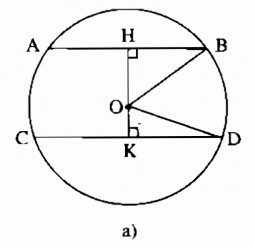
* Trường hợp O nằm giữa hai dây AB và CD (hình a):
HK = OH + OK = 15 + 7 =22 (cm)
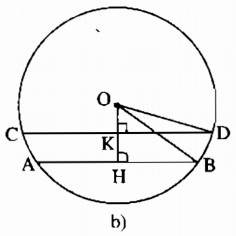
* Trường hợp O nằm ngoài hai dây AB và CD (hình b):
HK = OH – OK = 15 – 7 = 8 (cm).
