Advertisements (Quảng cáo)
Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:
a) OC là tia phân giác của góc AOB.
b) OC vuông góc với AB.
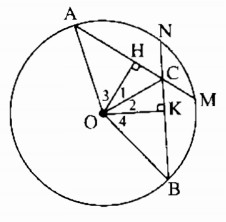
a) Kẻ OH ⊥ AM, OK ⊥ BN
Ta có: AM = BN (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCH và OCK, ta có:
\(\widehat {OHC} = \widehat {OKC} = 90^\circ \)
OC chung
OH = OK (chứng minh trên)
Suy ra: ∆OCH = ∆OCK (cạnh huyền, cạnh góc vuông)
Advertisements (Quảng cáo)
\(\widehat {{O_1}} = \widehat {{O_2}}\)
Xét hai tam giác OAH và OBK, ta có:
\(\widehat {OHA} = \widehat {OKB} = 90^\circ \)
OA = OB
OH = OK ( chứng minh trên)
Suy ra: ∆OAH = ∆OBK (cạnh huyền, cạnh góc vuông)
\(\widehat {{O_3}} = \widehat {{O_4}}\)
Suy ra: \(\widehat {{O_1}} + \widehat {{O_3}} = \widehat {{O_2}} + \widehat {{O_4}}\) hay \(\widehat {AOC} = \widehat {BOC}\)
Vậy OC là tia phân giác của \(\widehat {AOB}\)
b) Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân).
Suy ra: OC ⊥ AB.
Mục lục môn Toán 9 (SBT)