Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB >CD, chứng minh rằng MH > MK.. Câu 33* trang 161 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
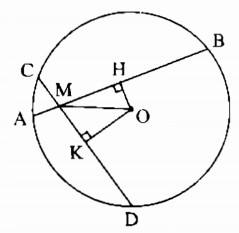
Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB >CD, chứng minh rằng MH > MK.
Ta có: HA = HB (gt)
Suy ra: OH ⊥ AB (đường kính dây cung)
Lại có: KC = KD (gt)
Suy ra: OK ⊥ CD ( đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH ( dây lớn hơn gần tâm hơn)
Advertisements (Quảng cáo)
Áp dụng định lí Pi-ta-go vào tam giác vuông OHM ta có:
\(O{M^2} = O{H^2} + H{M^2}\)
Suy ra: \(H{M^2} = O{M^2} - O{H^2}\) (1)
Áp dụng định lí Pi-ta-go vào tam giác vuông OKM, ta có:
\(O{M^2} = O{K^2} + K{M^2}\)
Suy ra: \(K{M^2} = O{M^2} - O{K^2}\) (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: \(H{M^2} > K{M^2}\) hay HM > KM.