Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Chứng minh rằng:
a) Điểm E nằm trên đường tròn(O);
b) DE là tiếp tuyến của đường tròn (O).

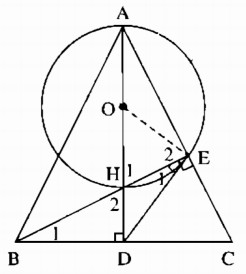
a) Gọi O là trung điểm của AH
Tam giác AEH vuông tại E có EO là đường trung tuyến nên:
\( EO = OA = OH ={{AH} \over 2}\) (tính chất tam giác vuông)
Vậy điểm E nằm trên đường tròn \(\left( {O;{{AH} \over 2}} \right)\)
b) Ta có: OH = OE
suy ra tam giác OHE cân tại O
suy ra: \(\widehat {OEH} = \widehat {OHE}\) (1)
Mà \(\widehat {BHD} = \widehat {OHE}\) (đối đỉnh) (2)
Advertisements (Quảng cáo)
Trong tam giác BDH ta có:
\(\widehat {HDB} = 90^\circ \)
Suy ra: \(\widehat {HBD} + \widehat {BHD} = 90^\circ \) (3)
Từ (1), (2) và (3) suy ra:
\(\widehat {OEH} + \widehat {HBD} = 90^\circ \) (4)
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
\(ED = BD = {{BC} \over 2}\) (tính chất tam giác vuông).
Suy ra tam giác BDE cân tại D
Suy ra: \(\widehat {BDE} = \widehat {DEB}\) (5)
Từ (4) và (5) suy ra: \(\widehat {OEH} + \widehat {DEB} = 90^\circ \) hay \(\widehat {DEO} = 90^\circ \)
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn ((O).
