a) Vẽ một lục giác đều ABCDEG nội tiếp đường tròn bán kính 2cm rồi vẽ hình 12 cạnh đều AIBJCKDLEMGN nội tiếp đường tròn đó. Nêu cách vẽ.
b) Tính độ dài cạnh AI.
c) Tính bán kính r của đường tròn nội tiếp hình AIBJCKDLEMGN.
Hướng dẫn. Áp dụng các công thức ở bài 46.
Giải
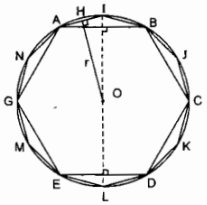
a) Cách vẽ:
− Vẽ đường tròn (0; 2cm)
− Từ điểm A trên đường tròn (0; 2cm) đặt liên tiếp các cung bằng nhau có dây trương cung 2cm.
\(\overparen{AB}\) = \(\overparen{BC}\) = \(\overparen{CD}\) = \(\overparen{DE}\) = \(\overparen{EG}\)
Nối AB, BC, CD, DE, EG, GA ta có lục giác đều ABCDEG nội tiếp trong đường tròn (0; 2cm).
Kẻ đường kính vuông góc AB và DE cắt đường tròn tại I và L.
Ta có: \(\overparen{AI}\) = \(\overparen{IB}\); \(\overparen{LD}\) = \(\overparen{LE}\)
Advertisements (Quảng cáo)
Kẻ đường kính vuông góc với BC và EG cắt đường tròn tại J và M.
\(\overparen{BJ}\) = \(\overparen{JC}\); \(\overparen{ME}\) = \(\overparen{MG}\)
Kẻ đường kính vuông góc với CD và AG cắt đường tròn tại N và K.
\(\overparen{KC}\) = \(\overparen{KD}\); \(\overparen{NA}\) = \(\overparen{NG}\)
Nối AI, IB, BJ, JC, CK, KD, DL, LE, EM, MG, GN, NA
Ta có đa giác đều 12 cạnh AIBJCKDLEMGN.
b) AI là cạnh của đa giác đều 12 cạnh.
Kẻ OH ⊥ AI
\(\widehat {IOH} = {{180^\circ } \over {12}} = 15^\circ \)
\(OI = {{HI} \over {\sin \widehat {IOH}}} \Rightarrow OI = {{AI} \over {2\sin \widehat {IOH}}} \Rightarrow AI = OI.2\sin \widehat {IOH}\)
AI = 2. 2sin 15º \( \approx \) 1,04 (cm)
c) OH = r bán kính đường tròn nội tiếp đa giác đều 12 cạnh. Trong tam giác vuông OHI ta có OH = OI.\({\rm{cos}}\widehat {HOI} = 2.c{\rm{os15}}^\circ \approx {\rm{1,93 (cm) }}\)
