Trong đường tròn (O; R) cho một dây AB bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp (Điểm C và điểm A ở cùng một phía đối với BO). Tính các cạnh của tam giác ABC và đường cao AH của nó theo R.
Giải
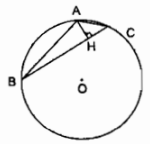
Dây AB bằng cạnh hình vuông nội tiếp đường tròn (O; R) nên AB = \(R\sqrt 2 \) và cung \(\overparen{AB}\) nhỏ có sđ \(\overparen{AB}\).
Dây BC bằng cạnh hình tam giác đều nội tiếp đường tròn (O; R) nên BC = \(R\sqrt 3 \) và cung nhỏ \(\overparen{BC}\) nhỏ có sđ \(\overparen{BC}\) \( = 120^\circ \).
\( \Rightarrow \) sđ \(\overparen{AC}\) = sđ \(\overparen{BC}\) - sđ \(\overparen{AB}\) = \(120^\circ - 90^\circ = 30^\circ \)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {ABC} = {1 \over 2}\) sđ \(\overparen{AC}\) = 150(tính chất góc nội tiếp)
Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow AH = AB.\sin \widehat {ABH} = R\sqrt 2 .\sin 15^\circ \approx 0,36R\)
Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)
\widehat {ACB} = {1 \over 2}\) sđ \(\overparen{AB}\) = 450 (tính chất góc nội tiếp)
\(AC = {{AH} \over {\sin \widehat {ACH}}} = {{AH} \over {\sin 45^\circ }} \approx {{0,36R} \over {\sin 45^\circ }} \approx 0,51R\)
