Một chiếc diều ABCD có AB = BC, AD = DC. Biết \(AB = 12cm,\widehat {ADC} = 40^\circ \)
\(\widehat {ABC} = 90^\circ \) (h.25)
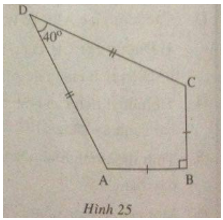
Hãy tính:
a) Chiều dài cạnh AD;
b) Diện tích của chiếc diều.
Gợi ý làm bài
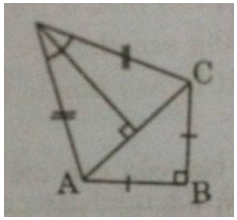
a) Nối AC và kẻ \(DH \bot AC\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} \cr
& = {12^2} + {12^2} = 144 + 144 = 288 \cr} \)
Suy ra: \(AC = 12\sqrt 2 \,(cm)\)
Ta có: tam giác ACD cân tại D
Advertisements (Quảng cáo)
\(DH \bot AC\)
Suy ra: \(HA = HC = {{AC} \over 2} = 6\sqrt 2 \,(cm)\)
\(\widehat {ADH} = {1 \over 2}\widehat {ADC} = 20^\circ \)
Trong tam giác vuông ADH, ta có:
\(\eqalign{
& {\rm{AD = }}{{AH} \over {\sin \widehat {ADH}}} \cr
& = {{6\sqrt 2 } \over {\sin 20^\circ }} \approx 24,809\,(cm) \cr} \)
b) Ta có:
\({S_{ABC}} = {1 \over 2}.AB.BC = {1 \over 2}.12.12 = 72\,\) (cm2)
Trong tam giác vuông ADH, ta có:
\(\eqalign{
& DH = AH.\cot g\widehat {ADH} \cr
& = 6\sqrt 2 .\cot g20^\circ \approx 23,313\,(cm) \cr} \)
Mặt khác:
\(\eqalign{
& {S_{ADC}} = {1 \over 2}.DH.AC \cr
& \approx {1 \over 2}.23,313.12\sqrt 2 = 197,817 \cr} \) (cm2)
Vậy Sdiều \(\eqalign{
& = {S_{ABC}} + {S_{ADC}} \cr
& = 72 + 197,817 = 269,817 \cr} \) (cm2)
