Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn ( C ∈ (O), D ∈ (O’)).
a) Tính số đo góc CAD.
b) Tính độ dài CD biết OA = 4,5cm, O’A = 2cm..

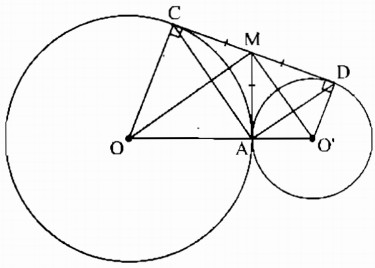
a) Kẻ tiếp tuyến chung tại A cắt CD tại M
Trong đường tròn (O) ta có:
MA = MC (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có:
MA = MD (tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(MA = MC = MD = {1 \over 2}CD\)
Advertisements (Quảng cáo)
Tam giác ACD có đường trung tuyến AM ứng với cạnh CD và bằng nửa cạnh CD nên tam giác ACD vuông tại A
Suy ra: \(\widehat {CAD} = 90^\circ \)
b) Ta có:
MO là tia phân giác của \(\widehat {CMA}\) (tính chất hai tiếp tuyến cắt nhau)
MO’ là tia phân giác của \(\widehat {DMA}\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra: MO ⊥ MO’ (tính chất hai góc kề bù)
Tam giác MOO’ vuông tại M có MA ⊥ OO’ ( tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
MA2 = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)
Mà \(MA = {1 \over 2}CD ⇒ CD = 2.MA = 2.3 = 6 (cm)\)
