Câu 8.1 trang 109 Sách Bài Tập (SBT) Toán 9 Tập 2
Mỗi câu sau đây đúng hay sai?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.
e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.
Giải
Câu a: Đúng Câu b: Sai Câu c: Sai
Câu d: Đúng Câu e: Đúng Câu f: Sai
Câu g: Đúng Câu h: Đúng Câu i: Sai
Advertisements (Quảng cáo)
Câu 8.2 trang 109 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB với đường tròn (O). Qua điểm M kẻ cát tuyến MCD với đường tròn (O) (tức là đường thẳng đi qua điểm M và cắt đường tròn tại hai điểm C, D). Gọi I là trung điểm của dây CD. Khi đó MAOIB có là ngũ giác nội tiếp hay không?
Giải
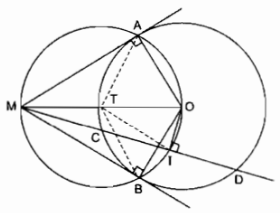
Khi cắt tuyến MCD không đi qua O.
IC = ID (gt)
\( \Rightarrow \) OI ⊥ CD (đường kính đi qua điểm chính giữa của dây không đi qua tâm)
\( \Rightarrow \widehat {MIO} = 90^\circ \)
MA ⊥ OA (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MAO} = 90^\circ \)
MB ⊥ OB (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MBO} = 90^\circ \)
A, I, B nhìn MO dưới một góc bằng 90º nên A, I, B nằm trên đường tròn đường kính MO.
Vậy: Ngũ giác MAOIB nội tiếp.
(Khi cắt tuyến MCD đi qua O ngũ giác MAOIB suy biến thành tứ giác MAOB chứng minh tương tự).
