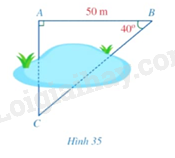
Dựa vào tỉ số lượng giác để giải bài toán. Giải và trình bày phương pháp giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn. Hình 35 mô tả ba vị trí \(A, B, C\) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ \(C\) đến \(A\) và từ \(C\) đến \(B\). Biết \(AB = 50m\)...

Hình 35 mô tả ba vị trí \(A,B,C\) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ \(C\) đến \(A\) và từ \(C\) đến \(B\). Biết \(AB = 50m\), \(\widehat {ABC} = 40^\circ \). Tính khoảng cách \(CA\) và \(CB\) (làm tròn kết quả đến hàng đơn vị của mét).

Dựa vào tỉ số lượng giác để giải bài toán.
Advertisements (Quảng cáo)

Xét tam giác \(ABC\) vuông tại \(A\), ta có:
+ \(BC = \frac{{AB}}{{\cos 40^\circ }} = \frac{{50}}{{\cos 40^\circ }} \approx 65\left( m \right)\).
+ \(AC = \frac{{AB}}{{\tan 40^\circ }} = \frac{{50}}{{\tan 40^\circ }} \approx 60\left( m \right)\).
