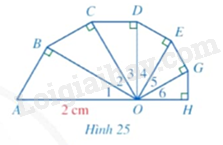
Tính độ dài đường gấp khúc \(ABCDEGH\), biết các tam giác \(OAB,OBC,OCD,ODE,OEG,OGH\) là các tam giác vuông tại các đỉnh lần lượt là \(B,C,D,E,G,H\); các góc \({O_1},{O_2},{O_3},{O_4},{O_5},{O_6}\) đều bằng \(30^\circ \) và \(OA = 2cm\) (Hình 25).
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Xét tam giác \(ABO\) vuông tại \(B\), ta có:
+) \(AB = AO.\sin 30^\circ = 2.\sin 30^\circ = 1\left( {cm} \right)\).
+) \(BO = AO.\cos 30^\circ = 2.\cos 30^\circ = \sqrt 3 \left( {cm} \right)\).
Xét tam giác \(BOC\) vuông tại \(C\), ta có:
+) \(BC = BO.\sin 30^\circ = \sqrt 3 .\sin 30^\circ = \frac{{\sqrt 3 }}{2}\left( {cm} \right)\).
+) \(CO = BO.\cos 30^\circ = \sqrt 3 .\cos 30^\circ = \frac{3}{2}\left( {cm} \right)\).
Xét tam giác \(COD\) vuông tại \(D\), ta có:
+) \(CD = CO.\sin 30^\circ = \frac{3}{2}.\sin 30^\circ = \frac{3}{4}\left( {cm} \right)\).
+) \(DO = CO.\cos 30^\circ = \frac{3}{2}.\cos 30^\circ = \frac{{3\sqrt 3 }}{4}\left( {cm} \right)\).
Xét tam giác \(DOE\) vuông tại \(E\), ta có:
+) \(DE = DO.\sin 30^\circ = \frac{{3\sqrt 3 }}{4}.\frac{1}{2} = \frac{{3\sqrt 3 }}{8}\left( {cm} \right)\).
+) \(EO = DO.\cos 30^\circ = \frac{{3\sqrt 3 }}{4}.\frac{{\sqrt 3 }}{2} = \frac{9}{8}\left( {cm} \right)\).
Xét tam giác \(EOG\) vuông tại \(G\), ta có:
+) \(EG = EO.\sin 30^\circ = \frac{9}{8}.\frac{1}{2} = \frac{9}{{16}}\left( {cm} \right)\).
+) \(GO = EO.\cos 30^\circ = \frac{9}{8}.\frac{{\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{{16}}\left( {cm} \right)\).
Xét tam giác \(GOH\) vuông tại \(H\), ta có:
\(GH = GO.\sin 30^\circ = \frac{{9\sqrt 3 }}{{16}}.\frac{1}{2} = \frac{{9\sqrt 3 }}{{32}}\left( {cm} \right)\).
Vậy độ dài đường gấp khúc \(ABCDEGH\) là:
\(ABCDEGH = 1 + \frac{{\sqrt 3 }}{2} + \frac{3}{4} + \frac{{3\sqrt 3 }}{8} + \frac{9}{{16}} + \frac{{9\sqrt 3 }}{{32}} = \frac{{37\left( {2 + \sqrt 3 } \right)}}{{32}}\left( {cm} \right)\).