Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 52
Bốn ô cửa hình vuông diện tích \(\frac{1}{2}{m^2}\) ghép thành cửa sổ Hình 1.
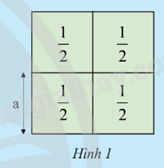
a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.

Kết quả của mỗi bạn có đúng không? Giải thích?
b) Biết rằng \(\sqrt 2 \approx 1,4142\). Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.
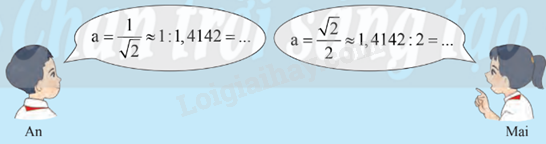
Theo em, bạn nào sẽ tìm ra đáp án nhanh hơn?

Dựa vào diện tích hình vuông: S = a2 với a là độ dài cạnh.

a) Diện tích một hình vuông: S = \(\frac{1}{2}\) (m2)
Mà S = a2 suy ra a = \(\sqrt S = \sqrt {\frac{1}{2}} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) (m)
Vậy kết quả của 2 bạn đều đúng.
b) Theo em, bạn An sẽ tìm đáp án nhanh hơn.
Vì bạn An chỉ cần tính \(\sqrt {\frac{1}{2}} = \frac{1}{{\sqrt 2 }}\).
Thực hành1
Trả lời câu hỏi Thực hành 1 trang 54
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }}\)
b) \( - \frac{{10}}{{3\sqrt 5 }}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\)

Dựa vào VD3 trang 53 làm tương tự.

Advertisements (Quảng cáo)
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }} = \frac{{\sqrt 7 .\sqrt 3 }}{{\sqrt 3 .\sqrt 3 }} = \frac{{\sqrt {21} }}{3}\)
b) \( - \frac{{10}}{{3\sqrt 5 }} = - \frac{{10.\sqrt 5 }}{{3\sqrt 5 .\sqrt 5 }} = - \frac{{10\sqrt 5 }}{{15}}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }} = \frac{{2\sqrt 2 .\sqrt {40} }}{{\sqrt {40} .\sqrt {40} }} = \frac{{8\sqrt 5 }}{{40}} = \frac{{\sqrt 5 }}{5}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\)\( = \frac{{\sqrt 2 .\left( {\sqrt 5 + \sqrt 2 } \right)}}{{\left( {\sqrt 5 - \sqrt 2 } \right).\left( {\sqrt 5 + \sqrt 2 } \right)}}\)\( = \frac{{\sqrt 2 .\left( {\sqrt 5 + \sqrt 2 } \right)}}{{{{\left( {\sqrt 5 } \right)}^2} - {{\left( {\sqrt 2 } \right)}^2}}}\)\( = \frac{{\sqrt 2 .\left( {\sqrt 5 + \sqrt 2 } \right)}}{{5 - 2}}\)\( = \frac{{\sqrt 2 .\left( {\sqrt 5 + \sqrt 2 } \right)}}{3}\)
Thực hành2
Trả lời câu hỏi Thực hành 2 trang 54
Khử mẫu của các biểu thức lấy căn:
a) \(\sqrt {\frac{{11}}{6}} \)
b) \(a\sqrt {\frac{2}{{5a}}} \) với a > 0
c) \(4x\sqrt {\frac{3}{{4xy}}} \) với x > 0; y > 0

Dựa vào VD2 trang 53 làm tương tự.

a) \(\sqrt {\frac{{11}}{6}} = \sqrt {\frac{{11.6}}{{6.6}}} = \frac{{\sqrt {66} }}{{\sqrt {{6^2}} }} = \frac{{\sqrt {66} }}{6}\)
b) \(a\sqrt {\frac{2}{{5a}}} = a.\sqrt {\frac{{2.5a}}{{5a.5a}}} = a\frac{{\sqrt {10a} }}{{\sqrt {{{(5a)}^2}} }} = a\frac{{\sqrt {10a} }}{{5\left| a \right|}}\) với a > 0
c) \(4x\sqrt {\frac{3}{{4xy}}} = 4x\sqrt {\frac{{3.4xy}}{{4xy.4xy}}} = 4x\frac{{\sqrt {12xy} }}{{\sqrt {{{\left( {4xy} \right)}^2}} }} = \frac{{8x\sqrt {3xy} }}{{\left| {4xy} \right|}}\) với x > 0; y > 0
Vận dụng1
Trả lời câu hỏi Vận dụng 1 trang 54
Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.
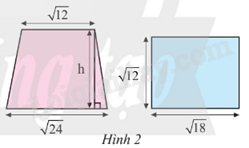

Dựa vào công thức diện tích hình chữ nhật S = a.b (a: chiều dài; b: chiều rộng), diện tích hình thang S = \(\frac{1}{2}(a + b).h\) (a và b: chiều dài hai cạnh đáy; h: chiều cao).

Ta có diện tích hình chữ nhật là: \(\sqrt {12} .\sqrt {18} = \sqrt {12.18} = \sqrt {216} = 6\sqrt 6 \)
Ta có diện tích hình thang bằng diện tích hình chữ nhật là: \(6\sqrt 6 \)
Mà diện tích hình thang là: \(\frac{1}{2}(\sqrt {12} + \sqrt {24} ).h\) = \(6\sqrt 6 \)
Suy ra h = \(\frac{{2.6\sqrt 6 }}{{(\sqrt {12} + \sqrt {24} )}} = 12 - 6\sqrt 2 \)
